Visualización de datos para centros territoriales

DatosRTVE

¡Hola!

¿Por qué incluir gráficos en las piezas?

Texto vs. gráfico

La empresa A tiene un beneficio anual de 100 millones de euros frente a la B, que ha logrado solo 75 millones.

  • Los números de un gráfico muestran la información de forma visual y narrativa
  • Refuerzan la idea que se quiere transmitir con el texto
  • Permite comparar los datos con un golpe de vista
  • Es un refuerzo visual o un complemento para la locución
  • “Un gráfico bien elegido vale más que mil palabras, proporciona comprensión y claridad en un mundo confuso” (Tim Harford, economista)

Para ofrecer contexto

El euribor está en el 4,074%

Para ofrecer contexto

El euribor está en el 4,074%, su nivel más elevado desde noviembre de 2008, tras el estallido de la burbuja inmobiliaria.

  • Un solo número no dice mucho, pero una serie en un gráfico puede contar una historia
  • Sirve para detectar y mostrar tendencias
  • Ofrecer referencias permite controlar el mensaje

Buenas prácticas para presentar datos, hechos y cifras

Los datos hablan por sí solos

“El mejor gráfico debe estar libre de cualquier distracción y permitirá que el lector compare y contraste los datos para sacar una conclusión”.

Dona M. Wong. Vicepresidenta de Comunicación del Banco de la Reserva Federal de Nueva York

Todo es relativo

Cuenta la historia completa

Cuenta la historia completa

Recuerda que...

El mensaje debe ser consistente con todos los datos relevantes para la historia

Haz comparaciones justas

Cuidado

Si dos gráficos se presentan juntos, se crea una comparación.

Haz comparaciones justas

Consejo

Usa escalas comparables. El eje de cada gráfico representa el mismo cambio porcentual para que la variación se perciba por la inclinación de las líneas.

Haz comparaciones justas

País Nº tarjetas de crédito (millones)
A 100
B 300
C 400

Haz comparaciones justas

País Nº tarjetas de crédito (millones)
A 100
B 300
C 400

Haz comparaciones justas

País Nº tarjetas de crédito (millones) Población (millones)
A 100 200
B 300 200
C 400 400

Haz comparaciones justas

País Nº tarjetas de crédito (millones) Población (millones) Nº tarjetas per cápita
A 100 200 0,5
B 300 200 1,5
C 400 400 1

Haz comparaciones justas

País Nº tarjetas de crédito (millones) Población (millones) Nº tarjetas per cápita
A 100 200 0,5
B 300 200 1,5
C 400 400 1

Consejo

Si los datos de origen son insuficientes ❌ No le añadas elementos decorativos ✅ Busca fuentes adicionales y ajusta los datos para hacerlos comparables

Haz comparaciones justas

  • Los números índices son útiles para realizar comparaciones de magnitudes en el tiempo o en el espacio.

  • Sirven para medir variaciones y permiten mostrar una evolución temporal o una comparación entre territorios fijando un valor como base.

  • El IPC no expresa precios en euros, sino las variaciones de esos precios el % para analizar su evolución a lo largo del tiempo.

Trata de mostrar la realidad

  • El propósito de un gráfico de líneas es mostrar una tendencia

  • Elegir una escala que aplana la curva desvirtúa el propósito del gráfico

  • Exagerar la escala crea un dramatismo que puede ser injusto con la realidad

Usa escalas naturales

Usa escalas naturales

¡Cuidado al truncar el eje!

  • Los gráficos de línea no siempre necesitan empezar en cero

  • Aunque hay que incluir la línea de base si los datos están cerca de ella

  • También es útil mostrar el 0 y el 100% con porcentajes

¡Cuidado al truncar el eje!

¡Cuidado al truncar el eje!

Cuidado

Los gráficos que muestran o comparan volúmenes entre sí siempre deben comenzar en cero

Ordena y reagrupa

  • La cualidad principal de un gráfico de barras es que crea un ranking

  • Ordenar las barras de mayor a menor (o viceversa) facilita la lectura

  • También puedes destacar una de las barras para reforzar el relato

Ordena y reagrupa

Hay algunas excepciones:

Leyendas y anotaciones

  • Una leyenda separada de las líneas obliga a trabajar más al espectador

  • Nunca incluyas anotaciones largas y utiliza solo las necesarias

Leyendas y anotaciones

  • Las etiquetas junto a las líneas permiten una identificación rápida y directa

  • Las anotaciones han de ser claras y concisas

Elige el gráfico apropiado para cada dato

¿Qué historia quieres contar?

Gráfico de línea

Si solo tienes una variable

Gráfico de áreas

Si tienes más de una variable y forman parte de un todo

Gráfico de líneas múltiple

Si tienes múltiples variables que no forman un todo pero comparten una unidad de medida

Gráfico de columnas

Magnitud en el tiempo

Columnas apiladas

stacked / treemap

Un todo y sus partes

Mapas de coropletas

Considerando la geografía

Diagrama de dispersión

Mostrar relación entre dos variables

Histograma

Para mostrar la distribución de una sola variable o de varias

Diagrama de Sankey

Muestra los flujos de un sistema

Diagrama de cuerdas

Muestra relaciones ponderadas y flujos entre nodos

Más info

Data Visualization Chart Cheatsheets | From data to viz |Visual Vocabulary

Gráficos de línea y área

  • Usa gráficos de líneas cuando quieras mostrar la evolución de unos datos

  • Los gráficos de líneas permiten comparar categorías entre sí

  • Si las categorías forman parte de un todo, es mejor el gráfico de área

  • Funcionan con series de datos largas que evolucionan de forma continua

  • Si tienes pocos datos, usa solo líneas rectas o elige columnas/barras

Gráficos de columnas/barras

  • Los gráficos de barras pueden ser simples o apiladas y pueden mostrar valores absolutos o relativos

  • Las columnas apiladas sirven para mostrar un todo y sus partes

  • Las barras o columnas apiladas se pueden usar con intervalos temporales, pero estos deben ser iguales

  • Los gráficos de área son una alternativa similar cuando los intervalos temporales son distintos

  • Elige las columnas si las etiquetas de los datos son cortas y las barras si son algo más largas

  • NUNCA incluyas el total en tu gráfico apilado, solo las partes que lo componen

Gráficos de columnas/barras

Gráficos de columnas/barras

Gráficos de columnas/barras

Gráficos de columnas/barras

Gráficos de columnas/barras

Gráficos de tarta/donut

  • Sirven para mostrar las partes en las de un todo (100%)

  • Funcionan mejor con datos alrededor del 25, 50 o 75%, más fáciles de reconocer

  • Reduce el número de valores agrupando las partes más pequeñas

  • Destaca el valor más importante y usa un degradado para el resto

  • Como en las líneas y las barras, coloca etiquetas directas en vez de leyenda

Gráficos de tarta/donut

  • Sirven para mostrar las partes en las de un todo (100%)

  • Funcionan mejor con datos alrededor del 25, 50 o 75%, más fáciles de reconocer

  • Reduce el número de valores agrupando las partes más pequeñas

  • Destaca el valor más importante y usa un degradado para el resto

  • Como en las líneas y las barras, coloca etiquetas directas en vez de leyenda

Consejo

Si pretendes que el lector compare el tamaño de cada parte, opta mejor por un gráfico de barras. Sobre todo si las diferencias son pequeñas

Gráficos de tarta/donut

Leer un gráfico de tarta es como leer un reloj, en el que puedes colocar los dos valores más grandes a la derecha y la izquierda de las 12 en punto.

Pictogramas

  • Los pictogramas ofrecen un vistazo rápido de cantidades y volúmenes, pero no sirven para mostrar datos masivos

  • Las barras son más eficientes para comparar cantidades discretas

  • Los iconos deben ser simples, simétricos y funcionar bien en tamaños pequeños

Mala elección

Buena elección

Pictogramas

No deformes los pictogramas para transformarlos en barras/columnas. El tamaño debe ser proporcional en cuanto al área.

Pictogramas

  • Utiliza unidades naturales.

  • Asigna un valor al icono y divide los datos en unidades que sean múltiplo de ese valor.

  • Evita partir los iconos. Si tus datos no encajan con esta división, las barras o las columnas son mejor opción.

Pictogramas

Si los datos que vas a comparar están muy juntos, no uses pictogramas.

Mapas

Tres tipos de mapas

Mapas coropléticos

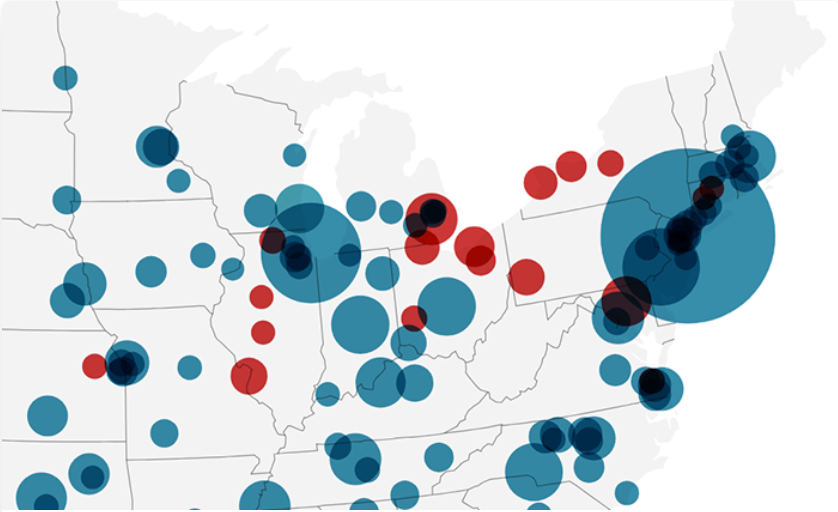
Mapas de símbolos

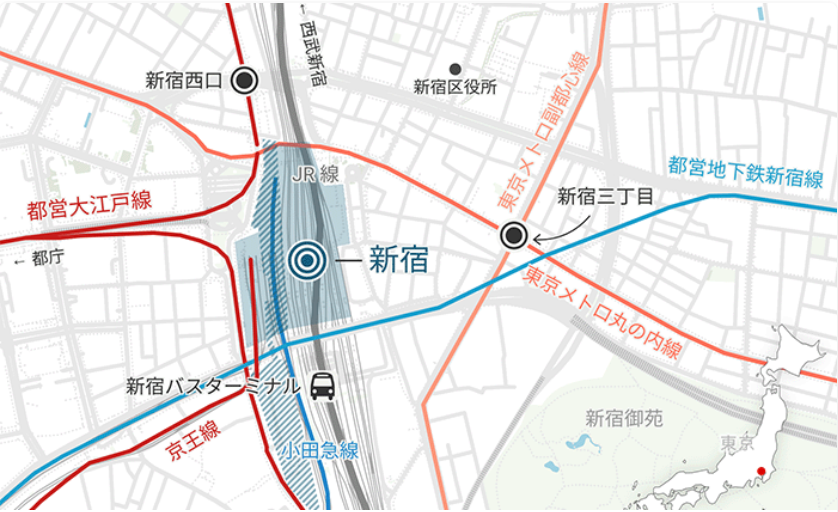
Mapa de ubicación

Mapas de coropletas

  • Ofrecen una visión general, pero dan poco detalle

Mapas de coropletas

  • Ofrecen una visión general, pero dan poco detalle

  • Útiles para mostrar/investigar un patrón geográfico en los datos

Mapas de coropletas

  • Ofrecen una visión general, pero dan poco detalle

  • Útiles para mostrar/investigar un patrón geográfico en los datos

  • Comparan una única variable que puede ser la diferencia entre dos valores

Mapas de coropletas

  • Ofrecen una visión general, pero dan poco detalle

  • Útiles para mostrar/investigar un patrón geográfico en los datos

  • Comparan una única variable que puede ser la diferencia entre dos valores

  • Funcionan mejor con datos relativos (Haz comparaciones justas)

Mapas de coropletas

Cada dato requiere una escala de color

Secuencial. Cuando tengas datos cuantitativos y quieras destacar los valores más altos

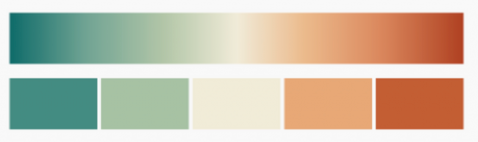
Divergente. Cuando tengas datos cuantitativos y quieras poner el foco en los dos extremos de la escala

Cualitativa o categórica. Cuando los datos no son cuantitativos

Algunas operaciones básicas

Algunas operaciones básicas

  • La mayoría de las matemáticas que se usan al hacer gráficos son operaciones básicas de álgebra y estadística

  • Las principales son:

    • Media

    • Mediana

    • Variación porcentual

Media, mediana y moda

  • Media. Suma de un conjunto de valores dividida entre el número total de sumandos

  • Mediana. Valor de la variable de posición central en un conjunto de datos ordenados

  • Moda. Valor que aparece con mayor frecuencia en un conjunto de datos

\[ Media = (1+2+3+3+4+7+7+7+11)/9 = 5 \]

Media vs. media ponderada

  • Media ponderada. Es apropiada cuando, en un conjunto de datos, cada uno de ellos tiene una importancia relativa (o peso) respecto de los demás

  • Se obtiene multiplicando cada uno de los datos por su ponderación (peso) para luego sumarlos; después se divide esta entre la suma de los pesos

Precio por acción ($) Nº acciones Precio * Peso
22 700 15.400
19 1.000 19.000
15 200 3.000
18 400 7.200
16 300 4.800
90 2.600 49.400

Media vs. media ponderada

Media simple

\[ sum(precios)/nº elementos \]

\[ 90/5 = 18$ \]

Media ponderada

\[ sum(precios*peso)/sum(pesos) \]

\[ 49.400/2.600 = 19$ \]

Precio por acción ($) Nº acciones Precio * Peso
22 700 15.400
19 1.000 19.000
15 200 3.000
18 400 7.200
16 300 4.800
90 2.600 49.400

Media vs. media ponderada

Recuerda que...

Aunque no cambie el precio de las acciones, una modificación en los pesos influye en la media

Media ponderada

\[ sum(precios*peso)/sum(pesos) \]

\[ 49.400/2.600 = 19$ \]

Precio por acción ($) Nº acciones Precio * Peso
22 700 15.400
19 1.000 19.000
15 200 3.000
18 400 7.200
16 300 4.800
90 2.600 49.400

Media móvil

Media móvil de cuatro días para ilustrar la tendencia subyacente

Variación porcentual

  • El cambio en los valores se puede expresar como un porcentaje a partir del dato original

  • Cuando el nuevo valor es más pequeño que el antiguo, el resultado es negativo

\[ Variación = ((nuevo - antiguo)/antiguo)*100 \]

Valores absolutos vs. cambios porcentuales

La representación de valores absolutos o de su cambio porcentual desde el dato de origen dibuja una curva de forma idéntica pero que atraviesa la línea de base

Expresar porcentajes

Porcentaje ≠ Puntos porcentuales ≠ Puntos básicos

  • Distintas formas de expresar un cambio en los valores:

    • Un incremento de 2 a 6 se puede expresar como…

    • … que el valor se triplica

    • … que el valor crece un 200%

  • La diferencia entre dos porcentajes se expresa como puntos porcentuales

    • Si un dato pasa del 2% al 1,75%…

    • …decrece 0,25 puntos porcentuales

  • También se puede expresar en puntos básicos

  • 1 punto porcentual = 100 puntos básicos

    • Si un dato pasa del 2% al 1,75%…

    • …decrece 25 puntos básicos

No hagas medias con porcentajes

Los porcentajes no se pueden tratar como números normales. Para hacer un promedio hay que volver a los datos originales.

Peligro

Media de A% y B% ≠ (A+B)/2

Recuerda que...

A% = c/e B% = d/f Nuevo porcentaje = ((c+d)/(e+f))*100

NOTA: Solo se pueden calcular medias de porcentajes si parten de la misma base. Por ejemplo, la nota media de una clase es la media simple del porcentaje aprobado de cada alumno, porque todos parten de 100%.

Fuentes recurrentes

Fuentes recurrentes

  • Dirección General de Tráfico.

  • Ministerio de Transportes y Movilidad Sostenible (MITMA).

  • Ministerio de Educación y de Universidades.

  • Fundación CYD.

  • Ministerio de Igualdad.

Bibliografía (I)

Bibliografía (II)

¡Gracias!

DatosRTVE • Visualización de datos para centros territoriales